Variational Autoencoders
Reference
Generative Deep Learning - Chapter 3
Autoencoders
An autoencoder is simply a neural network that is trained to perform the task of encoding and decoding an item, such that the output from this process is as close to the original item as possible. Crucially, it can be used as a generative model, because we can decode any point in the 2D space that we want.
Fashion-MNIST dataset
Fashion-MNIST is a dataset of Zalando’s article images—consisting of a training set of 60,000 examples and a test set of 10,000 examples. Each example is a 28x28 grayscale image, associated with a label from 10 classes. We intend Fashion-MNIST to serve as a direct drop-in replacement for the original MNIST dataset for benchmarking machine learning algorithms. It shares the same image size and structure of training and testing splits.
Link: https://github.com/zalandoresearch/fashion-mnist
Architecture
An autoencoder is a neural network made up of two parts:
- An encoder network that compresses high-dimensional input data such as an image into a lower-dimensional embedding vector
- A decoder network that decompresses a given embedding vector back to the original domain (e.g., back to an image)
The autoencoder is trained to reconstruct an image, after it has passed through the encoder and back out through the decoder. This may seem strange at first—why would you want to reconstruct a set of images that you already have available to you? However, as we shall see, it is the embedding space (also called the latent space) that is the interesting part of the autoencoder, as sampling from this space will allow us to generate new images.
The embedding ($z$) is a compression of the original image into a lower-dimensional latent space. The idea is that by choosing any point in the latent space, we can generate novel images by passing this point through the decoder, since the decoder has learned how to convert points in the latent space into viable images.
Let’s now see how to build the encoder and decoder.
Encoder
In an autoencoder, the encoder’s job is to take the input image and map it to an embedding vector in the latent space. To achieve this, we first create an Input layer for the image and pass this through three Conv2D layers in sequence, each capturing increasingly high-level features. The last convolutional layer is flattened and connected to a Dense layer of size 2, which represents our two-dimensional latent space.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import torch
import torch.nn as nn
## Define the Encoder class
class Encoder(nn.Module):
def __init__(self):
super(Encoder, self).__init__()
self.conv1 = nn.Conv2d(1, 32, kernel_size=3, stride=2, padding=1)
self.conv2 = nn.Conv2d(32, 64, kernel_size=3, stride=2, padding=1)
self.conv3 = nn.Conv2d(64, 128, kernel_size=3, stride=2, padding=1)
self.flatten = nn.Flatten()
self.fc = nn.Linear(128 * 4 * 4, 2) # Assuming shape_before_flattening is (4, 4)
def forward(self, x):
x = torch.relu(self.conv1(x))
x = torch.relu(self.conv2(x))
x = torch.relu(self.conv3(x))
x = self.flatten(x)
x = self.fc(x)
return x
## Create an instance of the Encoder
encoder = Encoder()
## Print the model summary
print(encoder)
This PyTorch code defines an encoder module with three convolutional layers followed by a flattening layer and a fully connected layer with 2 units. You can use this Encoder module as part of your autoencoder architecture.
Decoder
The decoder is a mirror image of the encoder—instead of convolutional layers, we use convolutional transpose layers.
The convolutional transpose layer uses the same principle as a standard convolutional layer (passing a filter across the image), but is different in that setting strides = 2 doubles the size of the input tensor in both dimensions.
In a convolutional transpose layer, the strides parameter determines the internal zero padding between pixels in the image, as shown in the figure below. Here, a 3 × 3 × 1 filter (gray) is being passed across a 3 × 3 × 1 image (blue) with strides = 2, to produce a 6 × 6 × 1 output tensor (green). 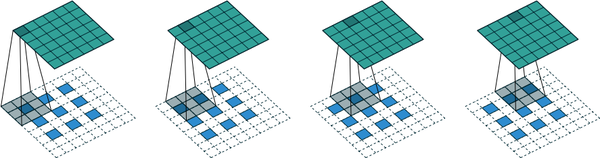
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import torch
import torch.nn as nn
## Define the Decoder class
class Decoder(nn.Module):
def __init__(self, shape_before_flattening):
super(Decoder, self).__init__()
self.fc = nn.Linear(2, shape_before_flattening[0] * shape_before_flattening[1] * shape_before_flattening[2])
self.reshape = nn.Unflatten(-1, shape_before_flattening)
self.conv1 = nn.Conv2d(128, 128, kernel_size=3, stride=1, padding=1)
self.conv2 = nn.Conv2d(128, 64, kernel_size=3, stride=2, padding=1, output_padding=1)
self.conv3 = nn.Conv2d(64, 32, kernel_size=3, stride=2, padding=1, output_padding=1)
self.conv4 = nn.Conv2d(32, 1, kernel_size=3, stride=1, padding=1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
x = self.fc(x)
x = self.reshape(x)
x = torch.relu(self.conv1(x))
x = torch.relu(self.conv2(x))
x = torch.relu(self.conv3(x))
x = self.sigmoid(self.conv4(x))
return x
## Define the shape_before_flattening variable
shape_before_flattening = (4, 4, 128) # Assuming shape_before_flattening is (4, 4, 128)
## Create an instance of the Decoder
decoder = Decoder(shape_before_flattening)
## Print the model summary
print(decoder)
This PyTorch code defines a decoder module with one fully connected layer followed by reshaping, and three transpose convolutional layers followed by a regular convolutional layer. Finally, a sigmoid activation function is applied to the output. We need to adjust the shape_before_flattening variable according to your encoder’s output shape.

