Generative Modeling

Reference

Generative Deep Learning - Chapter 1

Overview

Generative modeling can be broadly defined as follows:

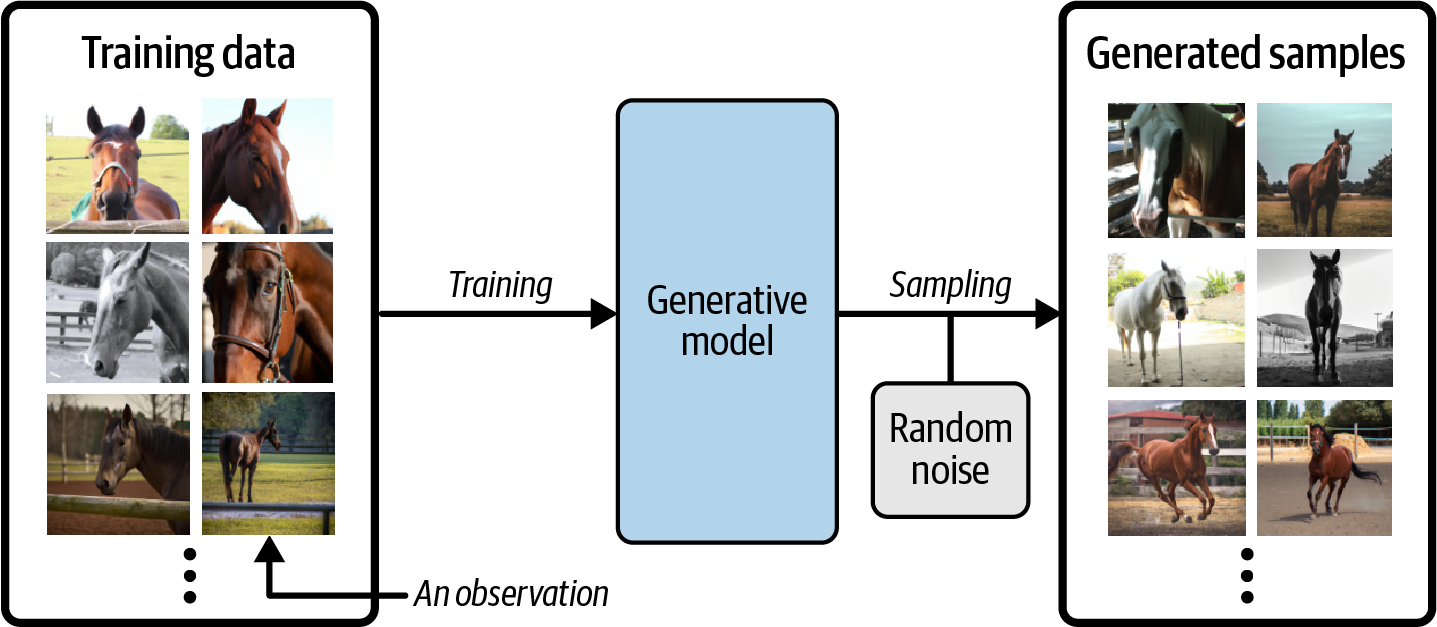
Generative modeling is a branch of machine learning that involves training a model to produce new data that is similar to a given dataset.

Suppose we have a dataset containing photos of horses. We can train a generative model on this dataset to capture the rules that govern the complex relationships between pixels in images of horses. Then we can sample from this model to create novel, realistic images of horses that did not exist in the original dataset.

A generative model must be probabilistic and not deterministic in nature since we want many different variations of the output rather than get the same output each time. To this end, we add a random noise while sampling to generate a different image each time.

Think of it this way, a generative model is like a creative dataset generator. Given a fixed set of images of horses, the generative model is able to create new images of horses by understanding what a horse should look like based on the input dataset.

Generative vs Discriminative

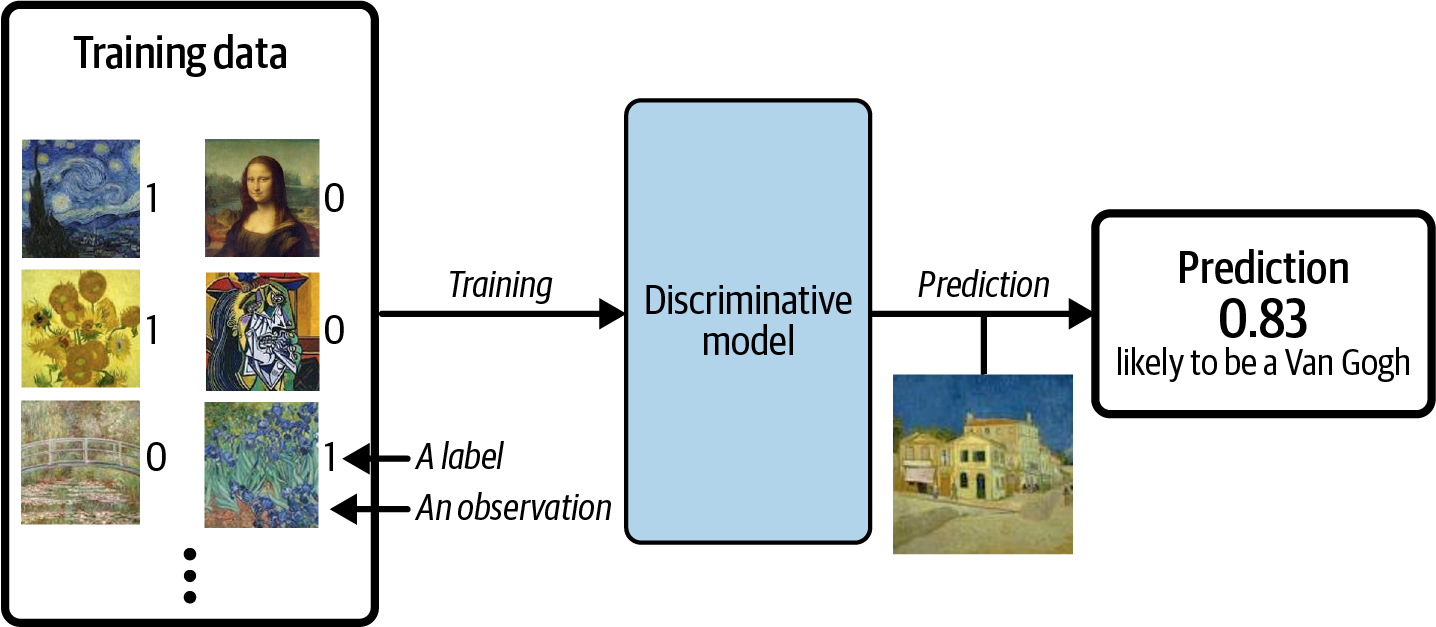
In order to understand generative modelling better like try to understand its more conventional counterpart, discriminative modelling.

Suppose we have a dataset of paintings, some painted by Van Gogh and some by other artists. We want to train a model that to predict if any given painting is done by Van Gogh or not. This is an example of discriminative modelling.

While training the model, the focus here is on understanding the patterns and characteristics of the dataset JUST ENOUGH to distinguish whether it’s made by Van Gogh or not.

Now image if we want to train a model that converts an input image into the style of Van Gogh. This will be a far more complex task for the model since it’d now have to learn ALL the features & characteristics that make up a Van Gogh painting and apply it on a input image leading to a significantly more complex task. Also unlike the deterministic model, the focus here is not on the label (whether Van Gogh or not) but the dataset itself!!

Discriminative modelling estimates ${p(y

x)}$ whereas generative modelling estimates $p(x)$

Representational Learning

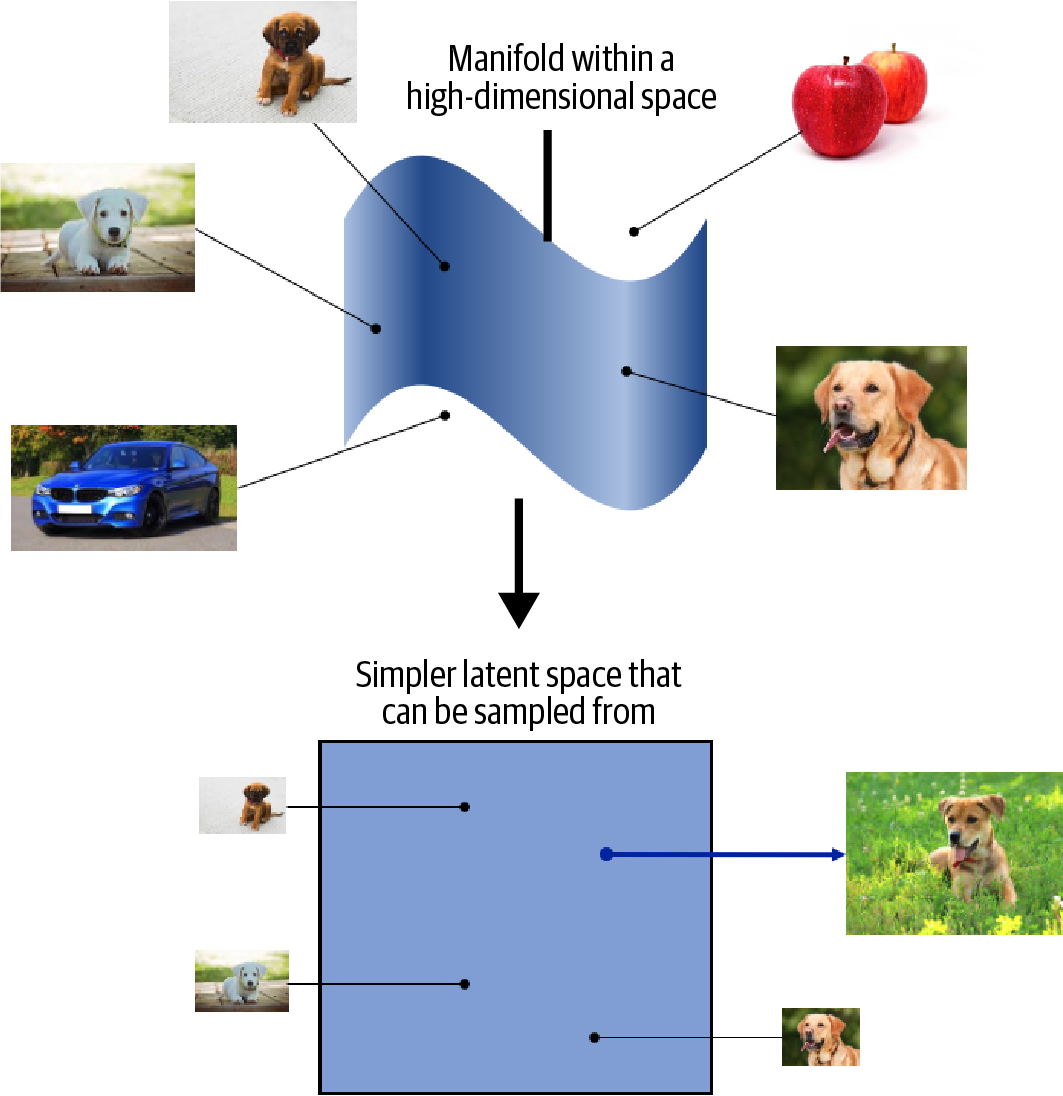
Learning the probabilistic distribution of a dataset can be challenging task owning to the high dimensionality of the space. This is where representational learning comes into play.

Suppose you wanted to describe your appearance to someone who was looking for you in a crowd of people and didn’t know what you looked like. You wouldn’t start by stating the color of pixel 1 of a photo of you, then pixel 2, then pixel 3, etc. Instead, you would make the reasonable assumption that the other person has a general idea of what an average human looks like, then amend this baseline with features that describe groups of pixels, such as I have very blond hair or I wear glasses. With no more than 10 or so of these statements, the person would be able to map the description back into pixels to generate an image of you in their head.

This is the core idea behind representation learning. 

Instead of trying to model the high-dimensional sample space directly, we describe each observation in the training set using some lower-dimensional latent space and then learn a mapping function that can take a point in the latent space and map it to a point in the original domain. In other words, each point in the latent space is a representation of some high-dimensional observation.

One of the benefits of training models that utilize a latent space is that we can perform operations that affect high-level properties of the image by manipulating its representation vector within the more manageable latent space.

The concept of encoding the training dataset into a latent space so that we can sample from it and decode the point back to the original domain is common to many generative modeling techniques. encoder-decoder techniques try to transform the highly nonlinear manifold on which the data lies (e.g., in pixel space) into a simpler latent space that can be sampled from, so that it is likely that any point in the latent space is the representation of a well-formed image.

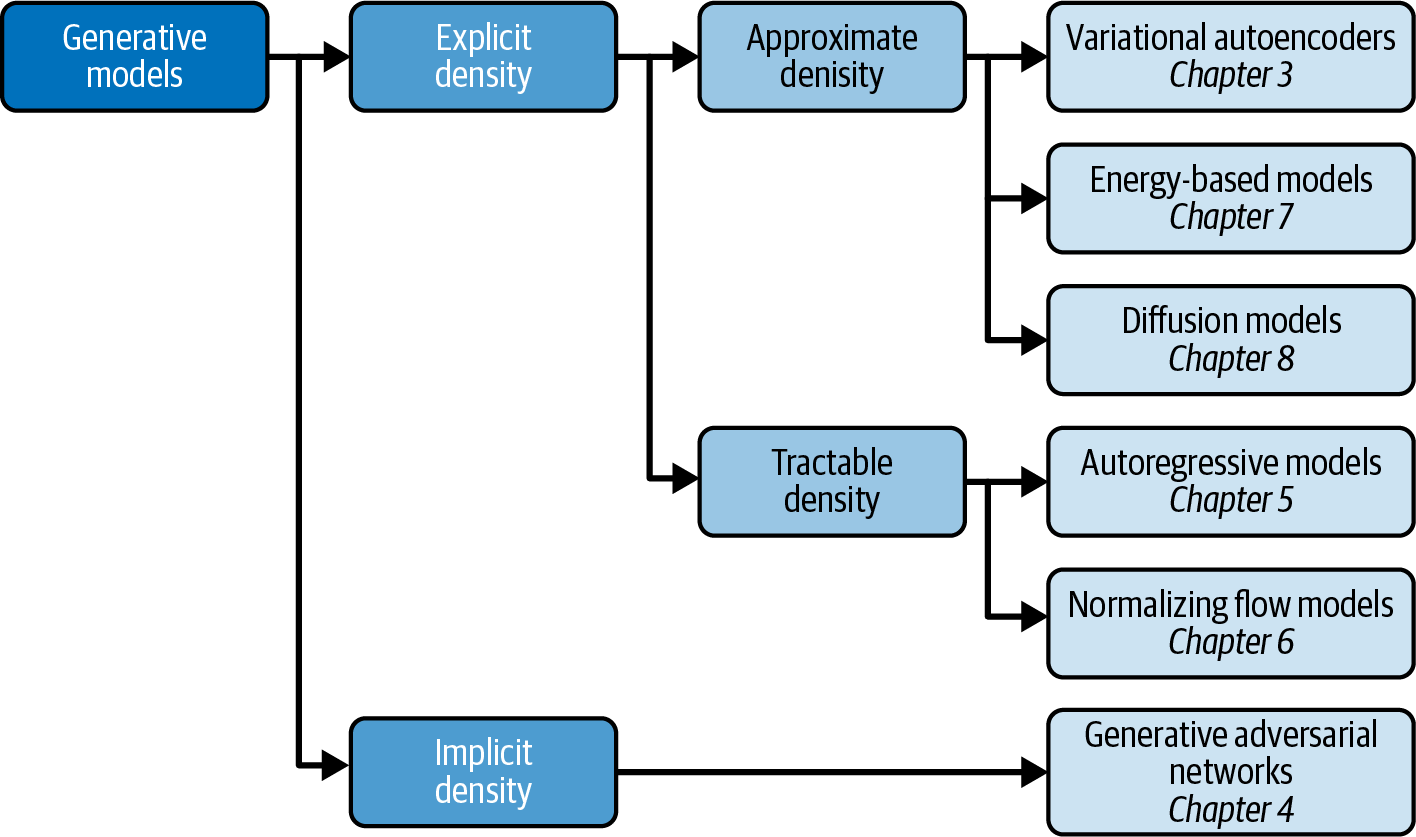
Generative Model Taxonomy

While all types of generative models ultimately aim to solve the same task, they all take slightly different approaches to modeling the density function $p_\theta(X)$ . Broadly speaking, there are three possible approaches:

1. Explicitly model the density function, but constrain the model in some way, so that the density function is tractable (i.e., it can be calculated).
2. Explicitly model a tractable approximation of the density function.
3. Implicitly model the density function, through a stochastic process that directly generates data.

Implicit density models do not aim to estimate the probability density at all, but instead focus solely on producing a stochastic process that directly generates data. The best-known example of an implicit generative model is a generative adversarial network.

Tractable models place constraints on the model architecture, so that the density function has a form that makes it easy to calculate.

Approximate density models include variational autoencoders, which introduce a latent variable and optimize an approximation of the joint density function. 

Energy-based models also utilize approximate methods, but do so via Markov chain sampling, rather than variational methods.

Diffusion models approximate the density function by training a model to gradually denoise a given image that has been previously corrupted.